Structured materials can exhibit mechanical properties that are unattainable in materials governed solely by their chemical composition. In some cases, conventional continuum models, such as the Cauchy continuum theory, must be extended to accurately describe the deformation behavior of certain metamaterials.
To explore this, we designed the pantographic orthoblock (see Figure 1), based on a unit cell composed of slender rods connected by pivots. These pivots enable deformations primarily driven by the bending of the rods. By incorporating second gradients of displacement into the continuum model, the pantographic orthoblock became the first three-dimensional metamaterial where higher-order gradient effects are the dominant deformation mechanism.
Generalized continuum theories, however, require specialized numerical methods due to the presence of additional degrees of freedom or the need to account for higher gradients, which demand more complex solution spaces. To address this, we developed a Finite Element routine based on Isogeometric Analysis, enabling the computation of deformation fields with well-defined second derivatives throughout the structure.
Additionally, the orthoblock demonstrates a large elastic range and exhibits semi-auxetic behavior (see Figure 2).
The pantographic orthoblock exemplifies the limitations of the traditional Cauchy continuum theory. To design and accurately describe truly novel metamaterials, more generalized and advanced theoretical frameworks are essential.
 |
| Figure 1: a 3D printed pantographic orthoblock. |
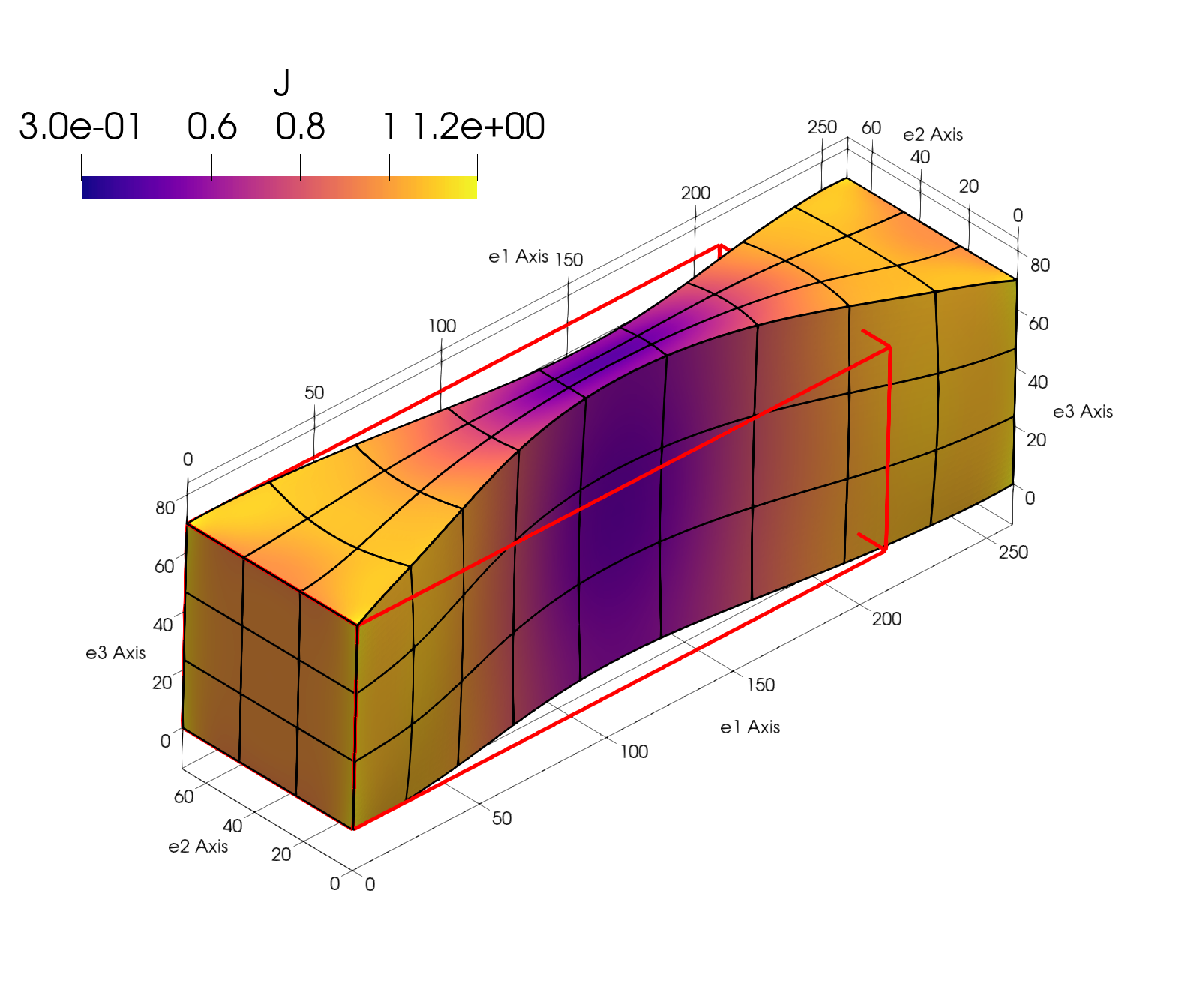 |
| Figure 2: a clamped extension test simulation showing the semi-auxetic behavior. |
associated publications:
- Antonina Trippel, Maximilian Stilz, Florian Gutmann, Georg C. Ganzenmueller, and Stefan Hiermaier. “A Device for Characterizing Rotational Joints in Metamaterials.” In: Mechanics Research Communications 104 (2020), p. 103501. issn: 0093-6413. doi: 10.1016/j.mechrescom.2020.103501.
- Maximilian Stilz, Francesco dell’Isola, Ivan Giorgio, Victor A. Eremeyev, Georg Ganzenmüller, and Stefan Hiermaier. “Continuum Models for Pantographic Blocks with Second Gradient Energies Which Are Incomplete.” In: Mechanics Research Communications 125 (2022), p. 103988. issn: 0093-6413. doi: 10.1016/j.mechrescom.2022.103988.
- Maximilian Stilz, David Plappert, Florian Gutmann, and Stefan Hiermaier. “A 3D Extension of Pantographic Geometries to Obtain Metamaterial with Semi-Auxetic Properties.” In: Mathematics and Mechanics of Solids 27.4 (2022), pp. 673–686. issn: 1081-2865. doi: 10.1177/10812865211033322.
- Francesco dell’Isola and Maximilian Stilz. “The «materialization» of Forces: Why Confounding Mathematical Concept and Physical Entity Makes the Design of Metamaterials Arduous.” In: ZAMM - Journal of Applied Mathematics and Mildunterschriftenechanics / Zeitschrift für Angewandte Mathematik und Mechanik 103.2 (2023), e202200433. issn: 1521-4001. doi: 10.1002/zamm.202200433.
- Florian Gutmann, Maximilian Stilz, Sankalp Patil, Frank Fischer, Klaus Hoschke, Georg Ganzenmüller, and Stefan Hiermaier. “Miniaturization of Non-Assembly Metallic Pin-Joints by LPBF-Based Additive Manufacturing as Perfect Pivots for Pantographic Metamaterials.” In: Materials 16.5 (2023), p. 1797. issn: 1996-1944. doi:10.3390/ma16051797.
- Maximilian Stilz, Francesco dell’Isola, and Stefan Hiermaier. “Complete 1D Continuum Model for a Pantographic Beam by Asymptotic Homogenization from Discrete Elements with Shear Deformation Measure.” In: Mechanics Research Communications 127 (2023), p. 104042. issn: 0093-6413. doi: 10 . 1016/j.mechrescom.2022.104042.
- Maximilian Stilz, Simon R. Eugster, Jonas Harsch, Florian Gutmann, Georg Ganzenmüller, and Stefan Hiermaier. “A Second-Gradient Elasticity Model and Isogeometric Analysis for the Pantographic Ortho-Block.” In: International Journal of Solids and Structures 280 (2023), p. 112358. issn: 0020-7683. doi: 10.1016/j.ijsolstr.2023.112358.
- Maximilian Stilz, Jonas Breuling, Simon Eugster, Marek Pawlikowski, and Roman Grygoruk. “Chirality Effects in Panto-Cylindrical Structures.” In: Mathematics and Mechanics of Solids (2024), p. 10812865231212145. issn: 1081-2865. doi: 10.1177/10812865231212145.



